Introduction
Circular Error Probability (CEP) is a statistical measure of accuracy used in targeting systems, representing the radius within which 50% of projectiles are expected to land.
Overview
CEP is a critical metric in assessing the accuracy of weapon systems, navigation systems, and other targeting technologies. It represents the radius of a circle centered on the intended target within which 50% of all projectiles or measurements are expected to fall. This metric provides a standardized way to quantify accuracy, making it useful for comparing different systems and for trade-off analysis in system design.
In the context of digital engineering, CEP serves as a key performance parameter (KPP) used to evaluate system effectiveness. It’s one of the primary metrics tracked through the digital thread to assess how well a system meets its intended mission objectives.
| CEP is a statistical measure that assumes a bivariate normal distribution of impact points. This means that the distribution of errors in the x and y directions follows a normal distribution, and the errors are uncorrelated. |
Position in Knowledge Hierarchy
Broader concepts: - MoE (is-a)
Details
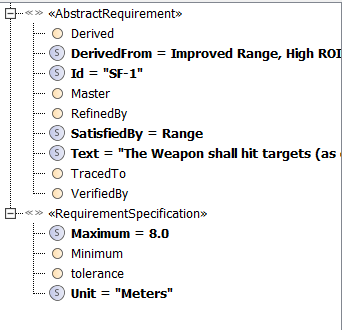
CEP is calculated using the following formula:
CEP = 0.6079 * σ
Where σ is the standard deviation of the impact points in a two-dimensional plane.
| The constant 0.6079 comes from the inverse of the cumulative distribution function for the Rayleigh distribution at the 50th percentile. |
CEP is related to other accuracy metrics:
Metric |
Relationship to CEP |
R95 (Radius containing 95% of impacts) |
R95 = 2.447 * CEP |
R99 (Radius containing 99% of impacts) |
R99 = 3.545 * CEP |
In the context of digital engineering and ontologies, CEP is one of the key parameters that needs to be properly modeled and tracked through the digital thread. In the Catapult example, CEP is used as a primary measure of effectiveness for the catapult system.
| In the IoIF framework, CEP must be properly tagged with the appropriate ontology terms to ensure it’s correctly interpreted and used in the analysis workflow. Failure to properly tag CEP can lead to inaccurate analysis results and poor decision-making. |
Practical applications and examples
The Catapult example provides a practical application of CEP in digital engineering:
-
Catapult Accuracy Analysis: In the Catapult use case, CEP is used to measure the accuracy of the catapult system in hitting a target. The system is analyzed under different variants (e.g., Analysis as Designed, Analysis as Manufactured, etc.) to determine how changes in design parameters affect CEP.
-
Trade-space Analysis: CEP is one of the key metrics used in the Decision Dashboard to evaluate different design alternatives. By tracking CEP across different variants, engineers can determine which design options provide the best balance of accuracy, cost, and other factors.
-
Integration with Ontologies: In the IoIF framework, CEP is represented as a value property in the SysML model, and must be properly tagged with ontology terms to ensure it’s correctly interpreted by the system.
Here’s an example of how CEP might be represented in a SysML model with ontology tagging:
CatapultSystem <<system>>
- CEP: ValueProperty <<circular_error_probability>>In the ontology, "circular_error_probability" would be a defined term that specifies the semantics of this metric. The Catapult ontology would include a class like:
:CEP a owl:Class ;
rdfs:label "Circular Error Probability" ;
rdfs:comment "A statistical measure of accuracy representing the radius within which 50% of projectiles are expected to land" .| In the Catapult example, CEP is one of the key parameters tracked in the Analysis Flow Diagram (AFD) that connects the system under analysis to various intermediate analysis models. |
Related wiki pages
References
Knowledge Graph
Associated Diagrams