Introduction
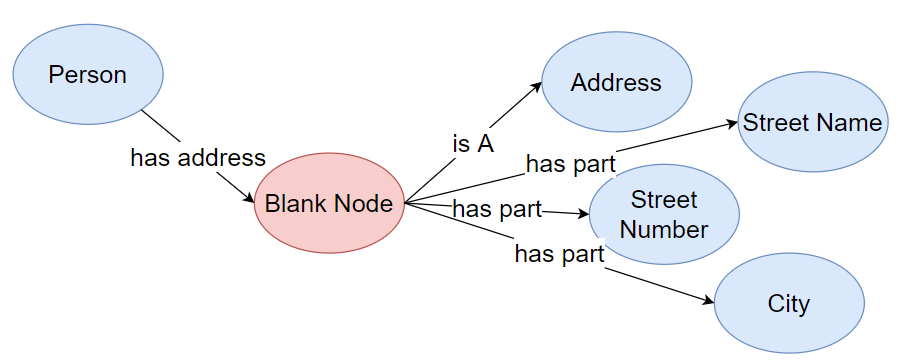
A Directed Acyclic Graph (DAG) is a type of graph where edges have direction and there are no cycles (no path that starts and ends at the same node). Imagine a flowchart where you can’t loop back to a previous step - that’s a DAG.
|
Think of a DAG as a "to-do list" where each task must be completed before the next one, and you can’t have a task that depends on itself or creates a circular dependency. |
Overview
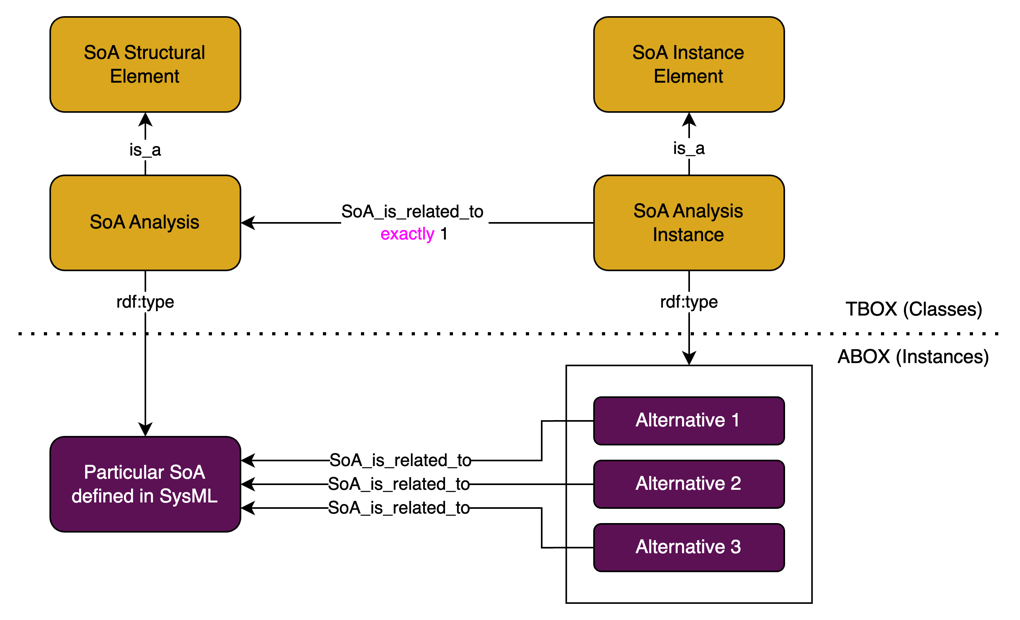
In Digital Engineering, a Directed Acyclic Graph (DAG) is a critical verification requirement for the System of Analysis (SoA). The SoA must form a DAG when ordered by sequence to ensure that the analysis workflow is logically consistent and free from circular dependencies. This requirement is essential for the proper functioning of the Assessment Flow Diagram (AFD) that represents the sequence of analyses in a multi-domain tradespace analysis.
The DAG requirement is one of the key model verification requirements for the SoA, specifically listed as Requirement 10 in the model requirements for the SoA:
Requirement 10: SoA shall form a Directed Acyclic Graph (DAG) when ordered by sequence
This requirement is verified using graph-based analysis, which is the third prong of the Semantic System Verification Layer (SSVL) for model verification.
Position in Knowledge Hierarchy
Broader concepts: - Graph-Based Analysis (is-a)
Details
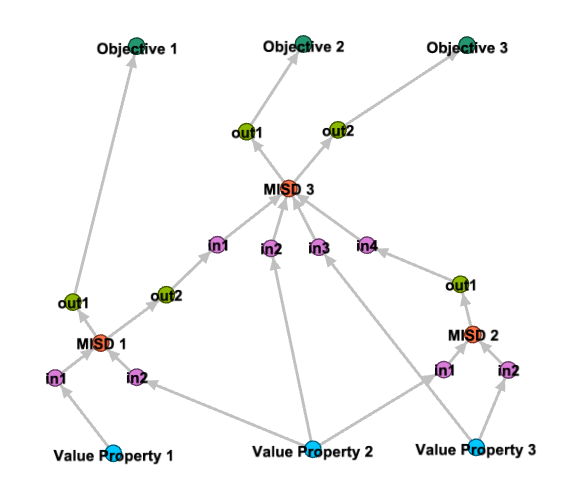
A Directed Acyclic Graph (DAG) is a graph data structure consisting of nodes (vertices) connected by directed edges (arrows), with the specific property that it contains no cycles. This means there is no path that starts and ends at the same node.
In the context of the System of Analysis (SoA), the DAG represents the sequence of analysis models and their dependencies. Each node in the DAG represents an analysis model or component, and each directed edge represents a dependency or data flow from one component to another. The absence of cycles ensures that the analysis sequence is logically sound and can be executed without encountering circular dependencies.
Key properties of DAGs relevant to SoA verification: * Directed: Edges have a specific direction (from source to target) * Acyclic: No cycles exist in the graph (no path that starts and ends at the same node) * Topological Ordering: Nodes can be ordered such that all edges point from earlier to later nodes in the ordering
The DAG property is critical for the SoA because: 1. It ensures that the analysis workflow has a well-defined sequence 2. It prevents circular dependencies that would make the analysis impossible to execute 3. It enables efficient computation of the analysis sequence 4. It supports the verification of the SoA’s structural integrity
|
The SoA DAG verification is performed using graph-based analysis tools like NetworkX, which can detect cycles in the graph representation of the SoA. |
Practical applications and examples
In the Digital Engineering context, DAGs are used to verify the structure of the System of Analysis (SoA) to ensure it can be executed without circular dependencies. The following example demonstrates this using the Catapult use case from the context.
Catapult Example Verification
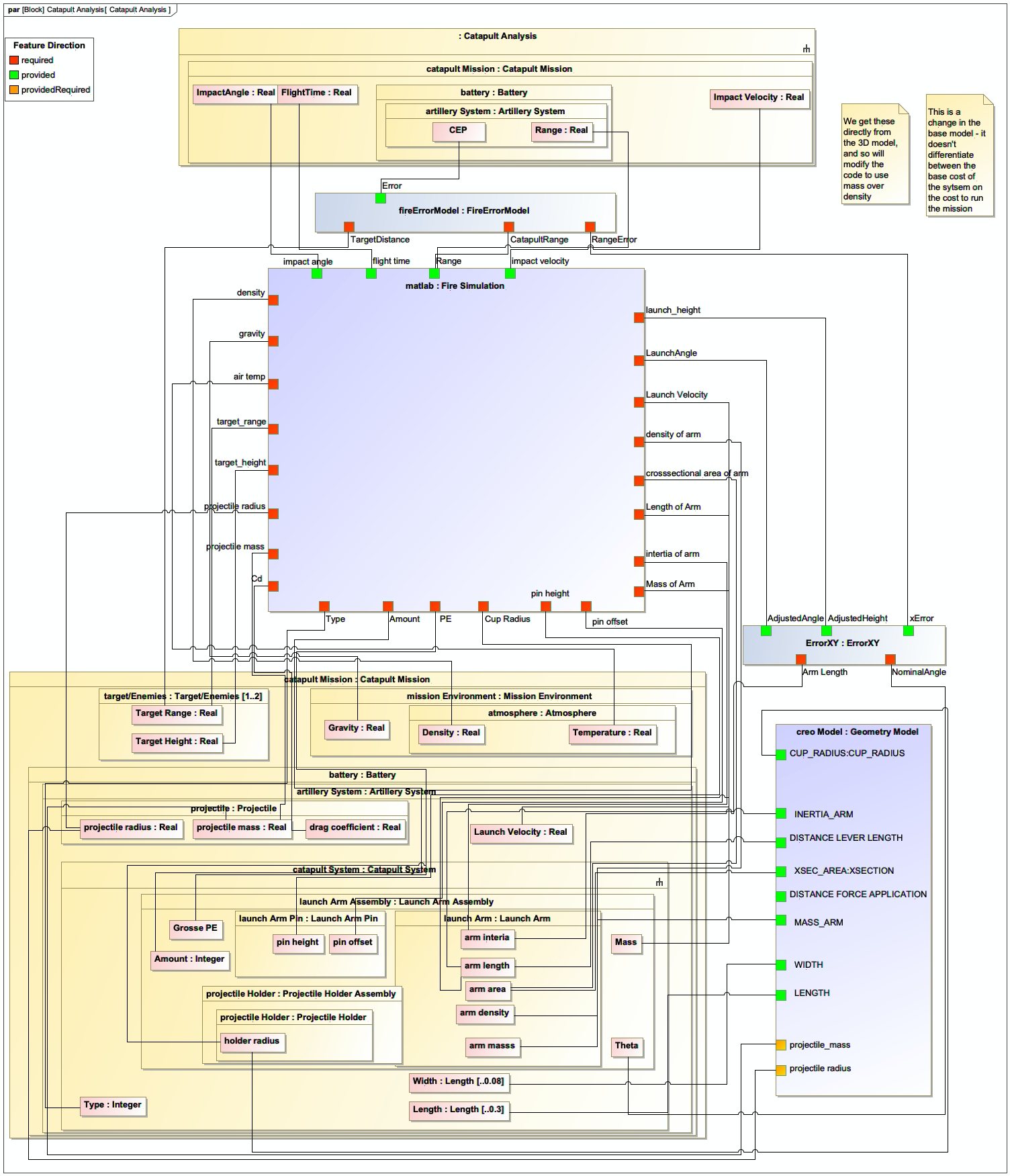
The Catapult example is used to demonstrate how DAG verification works in practice. The SoA for the Catapult model is represented as a graph where nodes represent analysis models and edges represent data flow between them.
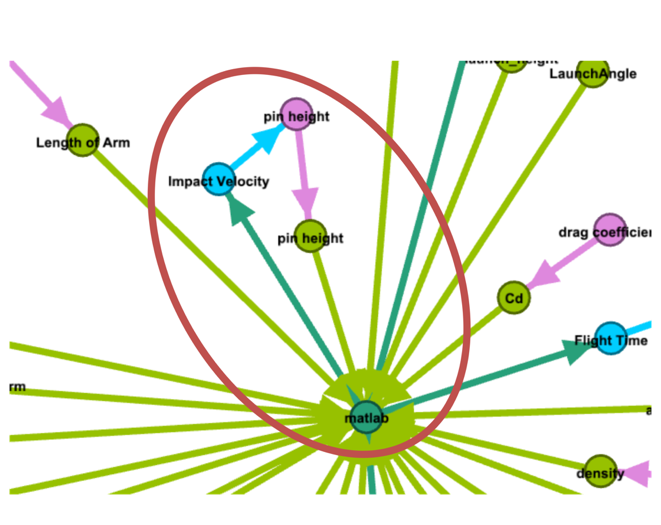
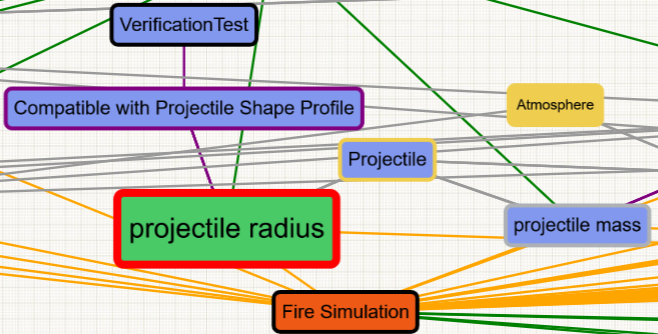
In the Catapult example, a cycle was intentionally inserted into the graph to demonstrate the verification process. The graph-based analysis detected this cycle as shown in Table 6:
Scenario Name |
Scenario |
Failure |
C26 |
Cycle from Impact Velocity to Pin Height |
Cycle Detected |
Figure 156 shows the portion of the Catapult AFD exhibiting the cycle that was detected by the graph analysis.
The verification process involves: 1. Extracting the SoA graph from the ontology-aligned data using SPARQL queries 2. Converting the extracted graph into a format suitable for graph analysis (e.g., using NetworkX) 3. Running a cycle detection algorithm on the graph 4. Reporting any cycles found as verification failures
|
The following Python code demonstrates how to use NetworkX to detect cycles in a graph, which is the core of the DAG verification process for the SoA: |
import networkx as nx
def is_dag(graph):
"""Check if a graph is a Directed Acyclic Graph (DAG)."""
try:
# Check for cycles
nx.find_cycle(graph)
return False
except nx.NetworkXNoCycle:
return True
= Example usage
G = nx.DiGraph()
G.add_edges_from([
('Impact Velocity', 'Pin Height'),
('Pin Height', 'Impact Velocity') # This creates a cycle
])
print("Is DAG:", is_dag(G)) # Should print "Is DAG: False"|
To verify the SoA as a DAG, the analysis workflow should:
1. Extract the SoA graph using SPARQL queries
2. Convert it to a NetworkX graph object
3. Use the |
|
When implementing DAG verification, ensure that: 1. The graph representation includes all nodes and edges from the SoA 2. The graph is correctly directed (edges have the right direction) 3. The cycle detection algorithm is appropriate for the graph size 4. All possible cycle paths are considered (not just simple cycles) |
Related wiki pages
References
DAG in SoA Verification
Associated Diagrams