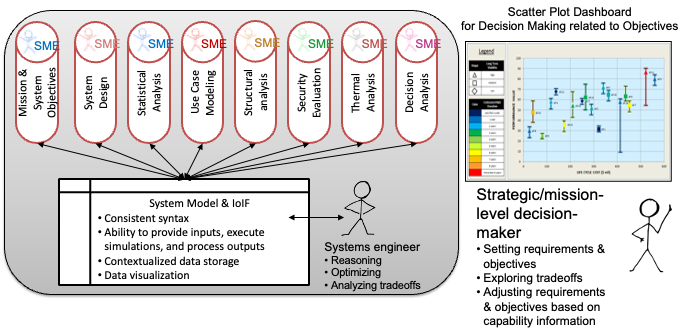
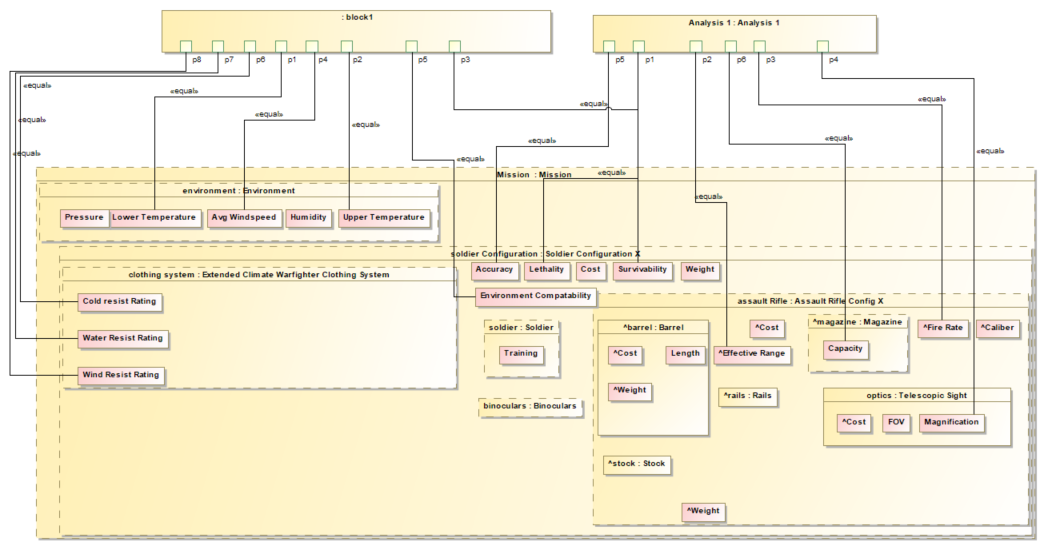
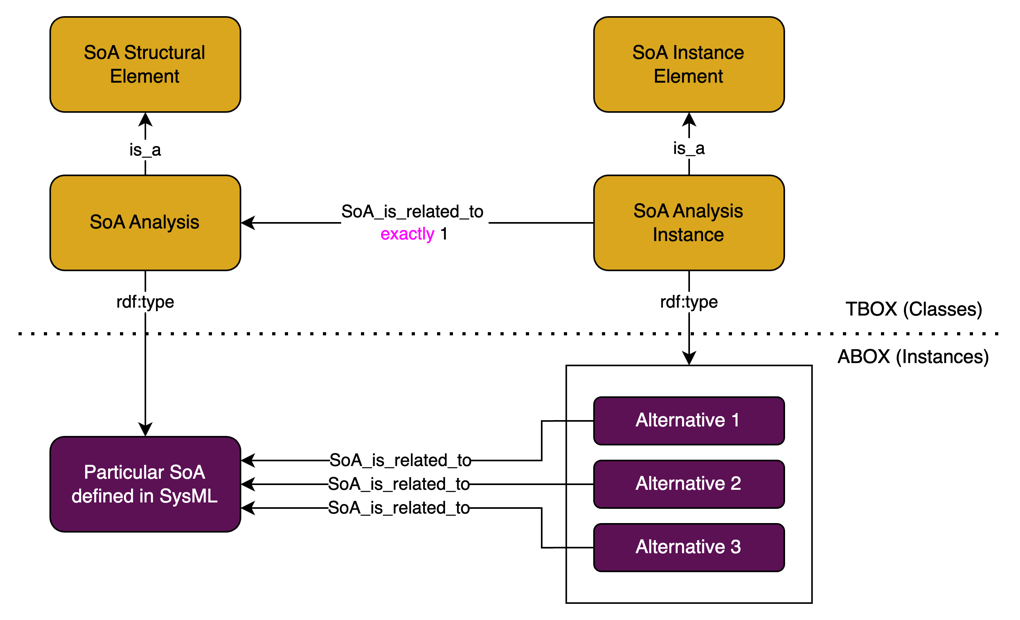
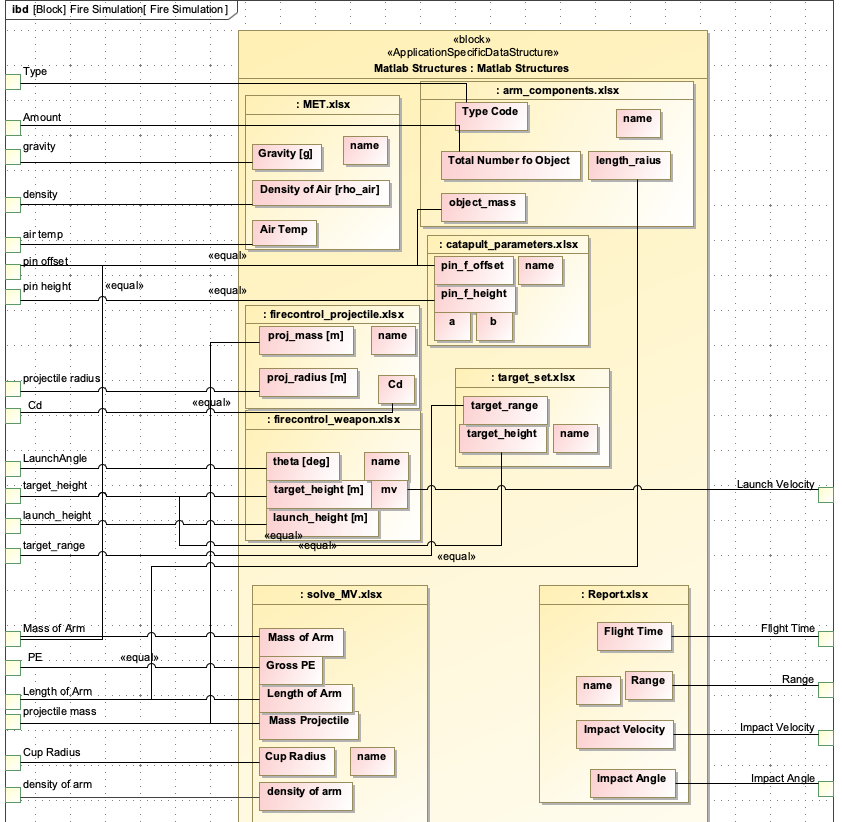
Introduction
The Semantic System Verification Layer (SSVL) is a critical component of the Digital Engineering Framework for Integration and Interoperability (DEFII) that enables automated model verification using ontology-aligned data. It ensures models are well-formed, consistent, and meet specified requirements through three complementary verification approaches.
Overview
The SSVL provides a robust framework for model verification in digital engineering by leveraging ontology-aligned data. It addresses the challenge of ensuring model quality and consistency across complex systems engineering workflows. The SSVL’s three-pronged approach ensures comprehensive verification coverage for a broad range of model requirements:
-
Open World Analysis: Uses Description Logic Reasoning for formal consistency checking
-
Closed World Analysis: Employs SHACL for constraint validation
-
Graph-Based Analysis: Applies graph algorithms to verify structural properties
This layered verification approach ensures models are well-formed and interoperable, which is essential for effective digital engineering workflows.
| The SSVL enables the verification of System of Analysis (SoA) models by checking them against specific requirements, ensuring they’re ready for use in trade space analysis and decision-making processes. |
Position in Knowledge Hierarchy
Broader concepts: - Part IV (is-a)
Narrower concepts: - Open World Assumption (is-a) - Closed World Assumption (is-a) - Graph-Based Analysis (is-a)
Details
The SSVL provides a systematic approach to model verification through three distinct verification approaches, each addressing different aspects of model quality.
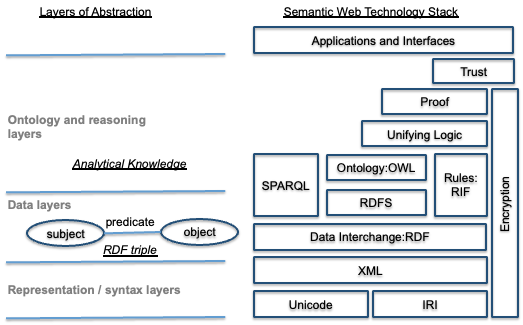
Open World Analysis (Description Logic Reasoning)
Open World Analysis uses Description Logic (DL) reasoning to check for consistency and infer new information based on the ontology. This approach operates under the Open World Assumption (OWA), where anything not explicitly stated is assumed to be unknown rather than false.
| DL reasoners like Pellet and HermiT are used to check for consistency and infer new facts based on the ontology’s axioms. This is particularly useful for checking logical constraints that must hold true in the model. |
The OWA approach has limitations in that it cannot verify the existence of required elements. For example, if a model should have a specific property, OWA cannot confirm it’s missing—it only knows it’s not explicitly stated.
| DL Reasoning Example: Verifying that a SportsUtilityVehicle has exactly 4 wheels would fail for a 3-wheeled SUV under OWA because the reasoner assumes a fourth wheel exists but it’s not explicitly stated. |
Closed World Analysis (SHACL)
Closed World Analysis uses the Shapes Constraint Language (SHACL) to perform constraint validation under a Closed World Assumption (CWA). This approach is used to verify the existence of required elements and enforce minimum/maximum cardinality constraints.
| SHACL is essential for verifying requirements that depend on the presence of specific elements or relationships. It provides a mechanism for "closing" the analysis context, which is necessary for many practical verification scenarios. |
SHACL defines constraints through shapes that specify what must be true about the data. These shapes can be applied to verify requirements like: - "Each SoA Connector shall be terminated at exactly two unique points" - "All value properties shall be tagged with a value in the loaded ontologies"
| SHACL is particularly valuable for verifying requirements that involve existence constraints, which cannot be verified using Open World Analysis alone. |
Graph-Based Analysis
Graph-Based Analysis applies graph algorithms to verify structural properties of the model. This approach leverages the fact that ontology-aligned data is inherently graph-based, making it suitable for applying well-known graph algorithms.
| Graph-Based Analysis is particularly useful for verifying properties like acyclicity, connectivity, and path constraints in the model. |
This approach involves: 1. Extracting a subgraph from the ontology-aligned data using SPARQL queries 2. Applying graph algorithms to the extracted subgraph 3. Verifying the structural properties of interest
The most common application is checking for Directed Acyclic Graph (DAG) properties, which is critical for ensuring analysis workflows have a valid sequence.
| Graph-based analysis requires transforming ontology-aligned data into a format suitable for graph analysis tools like NetworkX, which may require additional SPARQL queries. |
Practical applications and examples
The SSVL is applied to verify System of Analysis (SoA) models using a set of predefined requirements. The following table shows how different verification approaches are applied to specific requirements:
Requirement Number |
Requirement Description |
Verification Approach |
1 |
Termination points shall not connect to like points (input–input, output–output, value property–value property) |
DL Reasoning |
2 |
Each SoA Connector shall be terminated at exactly two unique points |
SHACL |
3 |
Each SoA Connector shall be connected to a minimum of one [model] element |
DL Reasoning, SHACL |
4 |
Models shall not connect to themselves |
SHACL |
5 |
At least one analysis objective shall be present |
DL Reasoning |
6 |
Tool specification shall be included |
SHACL |
7 |
All value properties shall be tagged with a value in the loaded ontologies |
SHACL |
8 |
Models shall be instantiated (there should be a value associated with every entry from the AFD) |
SHACL |
9 |
Constraint parameters shall be directional (in SysML—have [DirectedFeature] stereotype with provided or required applied) |
SHACL |
10 |
SoA shall form a Directed Acyclic Graph (DAG) when ordered by sequence |
Graph Analysis |
| The verification approach for each requirement is selected based on the nature of the requirement. Some requirements can be verified using multiple approaches, and the practitioner must decide which approach is most appropriate for their specific context. |
Example: Verifying a DAG Structure
One common verification task is ensuring that the System of Analysis (SoA) forms a Directed Acyclic Graph (DAG) when ordered by sequence. This is critical for ensuring that analysis workflows have a valid sequence without circular dependencies.
| To verify a DAG, the following steps are required: 1. Extract the relevant subgraph from the ontology-aligned data using SPARQL 2. Use a graph analysis library (like NetworkX) to check for cycles 3. Report any detected cycles for remediation |
Here’s an example Python code snippet demonstrating how to check for cycles using NetworkX:
import networkx as nx
from rdflib import Graph
= Load ontology-aligned data
g = Graph()
g.parse("soa_data.ttl", format="turtle")
= Create a directed graph
G = nx.DiGraph()
= Extract nodes and edges from the ontology
for s, p, o in g:
if p == "http://example.org/ontology/terminated_to":
G.add_edge(str(s), str(o))
= Check for cycles
if nx.is_directed_acyclic_graph(G):
print("SoA forms a valid DAG")
else:
# Find the cycle
cycle = nx.find_cycle(G)
print("Cycle detected in SoA:", cycle)| When using NetworkX for cycle detection, ensure the graph is properly constructed from the ontology-aligned data. Missing or incorrect relationships can lead to false positives or negatives in cycle detection. |
Example: Verifying Value Property Tagging
Another common verification task is ensuring all value properties are properly tagged with ontology terms. This is critical for ensuring data interoperability and consistency.
| The following SHACL shape can be used to verify this requirement: |
@prefix sh: <http://www.w3.org/ns/shacl#> .
@prefix ex: <http://example.org/ontology/> .
ex:ValuePropertyShape
a sh:NodeShape ;
sh:targetClass ex:ValueProperty ;
sh:property [
sh:path ex:taggedWith ;
sh:minCount 1 ;
sh:message "Value property must be tagged with an ontology term" ;
] .This SHACL shape ensures that every ValueProperty instance has at least one taggedWith value, verifying Requirement 7 from the example requirements table.
Related wiki pages
References
Shapes Constraint Language (SHACL) Specification
OWL 2 Web Ontology Language Overview
Protégé Ontology Editor
NetworkX Python Library
SPARQL 1.1 Query Language
OWL 2 Web Ontology Language Document Overview
A Three-Pronged Verification Approach to Higher-Level Verification Using Graph Data Structures
Driving Digital Engineering Integration and Interoperability Through Semantic Integration of Models with Ontologies
SSVL Relationship Diagram
Associated Diagrams