Introduction
A piecewise linear function used to normalize Key Performance Parameters (KPPs) to a standard 0-100 scale for decision analysis in the ISEDM methodology.
Overview
Value Functions are a core component of the Integrated Systems Engineering Decision Management (ISEDM) methodology, enabling the transformation of raw KPP measurements into standardized value metrics that reflect stakeholder preferences. Each Value Function is defined independently for a specific KPP and allows for meaningful comparison across diverse performance metrics. The function uses five key points to define the acceptable range of performance, with corresponding values on a 0-100 scale.
| Value Functions are used in conjunction with Swing Weights to calculate an overall performance score for each alternative in trade space analysis. |
Position in Knowledge Hierarchy
Broader concepts: - ISEDM (is-a)
Details
Value Functions are piecewise linear functions defined by five specific points that represent stakeholder preferences for a particular KPP. These points define the acceptable performance range and corresponding value metrics.
Point |
Description |
Walkaway Point |
The minimum acceptable performance level (value = 0) |
Marginally Acceptable |
The level where performance is just acceptable (value = 25) |
Target Value |
The desired performance level (value = 50) |
Stretch Goal |
The ambitious but achievable performance level (value = 75) |
Meaningful Limit |
The maximum performance level that provides significant value (value = 100) |
For a given KPP measurement (X), the corresponding value (V) is calculated through linear interpolation between the two nearest points in the value function. The calculation follows these steps:
-
Identify the two points that bracket the measurement
-
Calculate the difference between the measurement and the lower point
-
Divide by the range between the two points
-
Multiply by the value difference between the two points
-
Add to the value of the lower point
| Value Functions must be established through stakeholder preference elicitation by Subject Matter Experts (SMEs) to ensure they accurately reflect the true value of performance levels to decision-makers. |
Practical applications and examples
Let’s examine a practical example for the KPP "Range" in a catapult system:
Point |
Range (meters) |
Walkaway Point |
500 |
Marginally Acceptable |
750 |
Target Value |
1000 |
Stretch Goal |
1250 |
Meaningful Limit |
1500 |
For an alternative with a range of 1100 meters: 1. The measurement (1100) falls between Target Value (1000m, value=50) and Stretch Goal (1250m, value=75) 2. Difference from Target Value: 1100 - 1000 = 100 3. Range between points: 1250 - 1000 = 250 4. Fraction: 100/250 = 0.4 5. Value: 50 + (0.4 × (75-50)) = 50 + 10 = 60
Thus, the normalized value for Range would be 60.
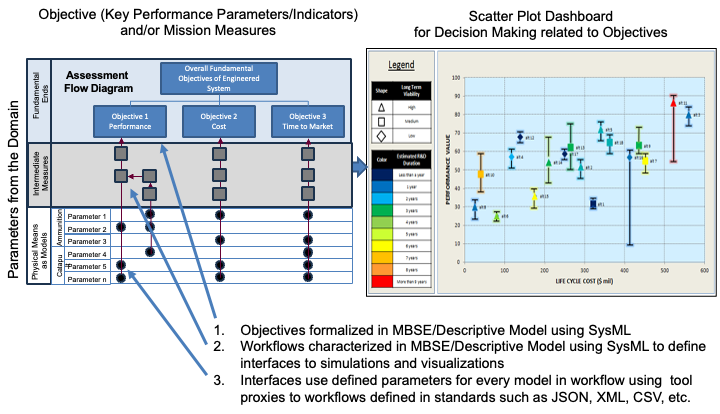
| The Decision Dashboard interface (Figure 136) provides an editable table for updating these five points. Changes to the value function points automatically update the visualization and recalculate the performance values for all alternatives. |
| When defining Value Functions, it’s important to have SMEs establish the five points based on their domain knowledge rather than using arbitrary values. This ensures the value function accurately reflects stakeholder preferences. |
| Value Functions should be established before trade space analysis begins, as they define how KPP measurements are converted to standardized values that will be used in the decision-making process. |
Related wiki pages
References
Knowledge Graph
Visualize the relationships between Value Functions and related concepts
Associated Diagrams